一点线性代数

学完就忘，重学。不过说实话，对于校内上的那种“线性代数”100以内四则运算忘不忘有意义吗。

和标题一样，就只有一点，而且组织混乱。

略过部分

• 线性相关
• Span
• ……

下面所有的内容都是基于向量空间内的意义。

行列式

行列式评价了一个线性变换对空间的放缩程度。对于一个二维空间，它就评价了对有向面积的放缩比例，三维则是体积。

所以对于行列式为0的变换，依照其意义，可以认为将空间进行了“降维”（压扁，但是它仍然在那个维度上）。那么这也是能够使用行列式判断一个向量组是否满秩（张成的空间和向量维数一致）的直观表现。

这同时也是可以使用行列式计算三维空间下的体积的直观表现，如果你把平行六面体理解成是单位立方体的变换。

$$ |M_1M_2|=|M_1||M_2| $$

基

基是向量空间中的概念，指的是一个可以张成向量空间$V$的线性无关向量组$\mathfrak {B}$。而对于一般情况下的有限向量空间，求解其基的方法就是从向量空间内依次删除线性相关项，直到其变为线性无关组。

其满足以下性质

• $V$是$\mathfrak {B}$的极小生成集，$\mathfrak {B}$的任何子集都无法张成$V$。
• $\mathfrak {B}$是$V$的极大线性无关组。

线性基

当计算为异或时，可以将整数以二进制分解作为向量，在这种意义下对这样的一个整数集合求基称为线性基。

其求法就像上文所说的求法，依次的考虑某一个整数是否限性相关。在实际编写时通过高斯消元来完成。

其具体思路为维护一个对角矩阵。由高位开始使用已有元素对新加入的元素进行消元，若完全消除，则线性相关；若未完全消除（由高位计算到第i位时无法消除），则将其计入基中，并使用所有剩余的低位对该元素对应位置继续消元，再使用该元素向上对先前的所有元素第i位进行消元。如此的复杂度$O(n\lg n)$。

由这个过程，我们能够得到的信息包含但不限于

1. 基：一组由原整数组组成的基，由消元过程判断。
2. 线性基：一组由原整数张成空间中的标准基。

一向量空间的所有基的长度相同，同时称为空间的维数。对于一个由n维的向量构成的向量空间，其维数不大于n。

Problem: Exclusive OR

Given $n$ integers $A_1,\cdots , A_n$. For all $1\leq i \leq n$, determine the maximum value by caculating xor of $i$ numbers that are repeatly chosen from $A$.

$$1\leq n \leq 2 \times 10^5, 0 \leq A_i < 2^{18}$$

利用异或卷积，令a[i]表示数i是否出现过，那么

$$ b_k=\sum_i\sum_j a_ia_j[i~\text{xor}~j =k] $$

即异或和为$k$的方案数。把$a$自己卷自己，统计每次卷完有方案的最大的$k$。

对于集合A，其张成的空间维数不可能超过18，则至多选择18个向量就可以构成其基，至多有18个向量就可以取到最大的xor。而从构成最大的向量开始，接下来就只是选择一个元素加入（所以至少算到19）和抵消，即每隔1个答案相同了。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79

#include <cstdio>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <vector>
#include <bitset>
#include <tuple>
using namespace std;
using ll = long long;
const int XN = 650000;
const int MOD = 998244353;
ll INV2 = 0;

ll qpow(ll x, ll a) {
    ll res = 1;
    for (; a; a >>= 1, x = (ll)x * x % MOD) {
        if (a & 1)res = (ll)res * x % MOD;
    }
    return res % MOD;
}

template<class T>
void FWT(ll a[], int n, T F) {
    for (int len = 2; len <= n; len *= 2)
        for (int i = 0; i < n; i += len)
            for (int j = i; j < i + len / 2; ++j)
                F(a[j], a[j + len / 2]);
}

void Txor(ll& x, ll& y) {
    auto a = (x + y) % MOD;
    auto b = (x - y + MOD) % MOD;
    x = a, y = b;
}

void Ixor(ll& x, ll& y) {
    auto a = (x + y) * INV2 % MOD;
    auto b = (x - y) * INV2 % MOD;
    x = a, y = b;
}
int ans[XN];
ll a[XN], b[XN];
int main() {
    ios::sync_with_stdio(false);
    INV2 = qpow(2, MOD - 2);

    int n;
    cin >> n;
    int maxx = 0;
    for (int i = 1; i <= n; i++) {
        int x; cin >> x;
        maxx = max(x, maxx);
        a[x] = 1;
        b[x] = 1;
    }
    int t = 1;
    while (t <= maxx)t *= 2;

    ans[1] = maxx;
    FWT(b, t, Txor);
    for (int i = 2; i <= 20; i++) {
        FWT(a, t, Txor);
        for (int i = 0; i <= t; i++) {
            a[i] = (ll)a[i] * b[i] % MOD;
        }
        FWT(a, t, Ixor);
        for (int j = t; j >= 0; j--) {
            if (a[j]) {
                ans[i] = j;
                break;
            }
        }
    }
    for (int i = 21; i <= n; i++)ans[i] = ans[i - 2];
    for (int i = 1; i <= n; i++)cout << ans[i] << " ";
    cout << endl;

    return 0;
}

线性变换

这里主要考虑通过矩阵对向量空间进行线性变换。考虑的办法主要是基于对基的操作。通过将某一个变换拆解为单一动作的矩阵，我们能够方便的去玩空间。

例如，计算三维空间中的某个点P按一条线$A$为轴旋转$\gamma$度后的位置。一个粗暴的思路是先将$x$轴转到$A$上去，计算$P$于原位置在新的基下的坐标$P'$，对$P'$以$x$轴旋转$\theta$度，对此时的$P'$重新逆回原基下的坐标。

以三维直线在$x-y$平面上的投影和$x$轴正半轴的夹角为$\theta$，以直线与$z$轴正半轴的夹角为$\phi$，那么首先以$\theta$旋转，再以$\phi$旋转即可把$x$轴转到$A$上去。两次旋转的变换矩阵分别为

以z轴旋转。

$$ M_z=\begin{bmatrix} \cos \theta & -\sin \theta & 0 \cr \sin \theta & \cos \theta & 0 \cr 0 & 0 & 1 \end{bmatrix} $$

以y轴旋转

$$ M_y=\begin{bmatrix} \sin \phi & 0 & -\cos \phi \cr 0 & 1 & 0 \cr \cos \phi & 0 & \sin \phi \end{bmatrix} $$

在此时，对于由$\Omega$以$M$变换到的$\Omega'$，在$\Omega'$空间下的坐标左乘变换$M$就能得到其在$\Omega$的坐标。$M$即为$\Omega'$和$\Omega$之间的桥梁。

那么，考虑如何将二者复合。首先执行z轴旋转，将$x$转到$A$在$x-y$平面上的投影位置，得到空间$\Omega'$。而后，我们需要对在$\Omega$下$\Omega'$的基在$\Omega'$下的坐标再次执行$y$轴旋转将其最终转到$A$上去，称为空间$\Omega_1$，再把$\Omega'$下的$\Omega_1$的基换算回$\Omega$里，准备进行下一步的转换。这个过程即

$$ M_zM_y(M_z^{-1}M_zI)=M_zM_y $$

然后计算$P$位于$\Omega_1$下的坐标，即求解$MP'=P \implies P'=M^{-1}P$，计算$|M|$恒非$0$，则$P'$总可求出。而后对$P'$执行以$x$轴（即A）旋转题目给定的$\gamma$角。再次计算$MP'$求出$P$即为答案。

以$x$轴旋转

$$ M_x=\begin{bmatrix} 1 & 0 & 0 \cr 0 & \cos \gamma & \sin \gamma \cr 0 & -\sin \gamma & \cos \gamma \end{bmatrix} $$

这几个矩阵简单画一下图就可以推出来。逆矩阵使用高斯消元处理伴随矩阵即可。

当线性变换找不到逆时，即我们的变换对空间做了降维。此时显然我们只能由$\Omega_1$中的坐标找到其在原空间下的对应，但是反过来则“几乎”做不到，而对于恰好存在映射的原空间点，也对应着新空间内的多个点，没有唯一答案。

另一个比较特殊的变换是高维向低维的转换。比如

$$ \begin{bmatrix} 1 & 3 & 5 \cr 2 & 4 & 6 \end{bmatrix} $$

这玩意会把三维直接映射成平面，你可以认为新的空间在原空间的$x-y$平面。

另一个更特殊的是低维向高维的转换。

$$ \begin{bmatrix} 1 & 4 \cr 2 & 5 \cr 3 & 6 \end{bmatrix} $$

这东西就有些与众不同了，它把原空间射到了新空间里。因为它是满秩的，没有降维之说，所以原空间内的任意一个点都可以在新的空间里找到对应；反过来显然（当然我是指值域而不是陪域）。

还有另一种比较不那么暴力的思路，就是通过上面这个东西去转点。以轴为法向量，确定一个经过点P的面，并在这个面上找两个基，把P转到这个基所确定的二维平面上，并在这个面上转P。对于法向量$n$，我们能找到$\vec P$以该法向量的平行与垂直部分。

$$ \begin{aligned} \vec p_{\parallel}&=(\vec n \cdot \vec p)\vec n \cr \vec p_{\perp}&=\vec p - \vec p_{\parallel} \end{aligned} $$

$\vec p_{\perp}$就是位于该平面内的一个可用基，同时$\vec p_{\parallel}$部分在旋转中不会发生变化。此时再找一个基就可以了。一般来讲，找它的垂直向量即可，也就是

$$ \begin{aligned} \vec w = \vec n \times \vec p &\iff \vec n \times (\vec p_{\parallel} + \vec p_{\perp}) \cr &\iff \vec n \times \vec p_{\perp} \end{aligned} $$

所以说，恰好构造的两个基$\vec p_{\perp}, \vec w$正交且等长（其实不等长正交又怎么样，我们只是去转一转，也无所谓）。使用变换$B=[\vec p_{\perp}, \vec w]$，就能实现把平面上的一个点🐍到原空间。……但这东西显然没逆矩阵，这意味着什么我还没搞明白，简单说显然原空间里只有那一个面可以找到对应点，但我总觉得缺了点什么。庆幸的是，这种基的找法使得$\vec p$在新空间里就对应着$\begin{bmatrix} 1 \cr 0 \end{bmatrix}$。

我们仍然考虑如何在平面内旋转，那么就是简单的去旋转$\vec p_{\perp},\vec w$即可。旋转的变换自然是刻在DNA里的变换矩阵，可以用复平面更方便的推出来。

$$ M=\begin{bmatrix} \cos \theta & -\sin \theta \cr \sin \theta & \cos \theta \end{bmatrix} $$

由此能够确定一个更加方便的转换

$$ BM\begin{bmatrix} 1 \cr 0 \end{bmatrix} $$

那么旋转后的$\vec p$在

$$ \vec p_{\parallel}+BM\begin{bmatrix} 1 \cr 0 \end{bmatrix} $$

这结果就漂亮多了。

线性方程组

依靠上文的线性变换意义，我们能够以这种视角去看待一个线性方程组。

$$ A\vec x = \vec v $$

A即描述了对空间$Omega$的一个变换，我们需要找到在新的空间下v的坐标。

再来看A降维的情况。此时，$\Omega_1$仅在$\Omega$下占一部分空间，对于该空间外的点均找不到解，该空间内的点能找到多个解。这是直观的解读，解组成的空间子集又称为零空间。

两种不同的看待角度

如果你把变换后的空间铺在原空间内，你可以把一个属于原空间的坐标看作拉伸到现有的位置。另一个看法是属于新空间的坐标向原空间的映射。我更喜欢后一种，在上面的描述中它也带来了方便。

我们能够这样去描述这个问题，是基于一个的事实：“我们不知道对方的坐标系是什么样子”。你不能说我选择一个基是斜着的，那它就是“斜着的”，这是基于你的坐标系来看待我的。尽管二者选择的基向量不同，但在二人看来，他们的空间均“很正常”。当二者相互交流时，上面的情况才会遇到。有点像一门语言翻译到另一门中，我们只能在二者间找到一个对应的关系（因为我们所处的世界相同，所以语言中大概率有相同概念），要么把你的对应到对方，要么把对方的对应到你，而$M$就是这里的翻译。只是恰好由于我们这里的变换后空间是从原空间衍生的，所以我们总能把新空间坐标对应到原空间内。把新空间画到原空间内意义就在于“新空间坐标在原空间的位置”。

“凭什么说我们的坐标系是从你的变换过来的，大热天我气的浑身发抖，手脚冰凉，眼泪止不住的流，我们什么时候才能站起来。”

如果你没懂的话那大概率也没明白上文的点旋转。

这是几个帮助你和我理解的问题：对于三维正交坐标系$\Omega$来讲，如果$\Omega'$是从$\Omega$变换过来的，

• 如何旋转$\Omega$下的一个向量？
• 如何旋转$\Omega'$下的一个向量？
• 如何将$\Omega'$的向量在$\Omega$下旋转？
• 如何将$\Omega$的向量在$\Omega'$下旋转？这种旋转什么时候才有意义，和上一个有什么区别？

点积&叉积

这个目测没什么用，但是仍然可以在空间和线性变换下解释。

对于$\vec u \cdot \vec v$，假设其都为2维的向量，那么我们在平面上讨论这个计算的意义。

将u描述为单位向量$k\vec e$，现有空间以$k\vec e^T$进行变换，观察变换意义。

$$ k\vec e^T\begin{bmatrix} 1 & 0 \cr 0 & 1 \end{bmatrix}=k\vec e^T $$

虽然结果没有任何变化，但此时其意义为变换后的空间基，分别为单位向量在x和y轴上的投影长，而且发生了降维。再来看二者数值的意义。

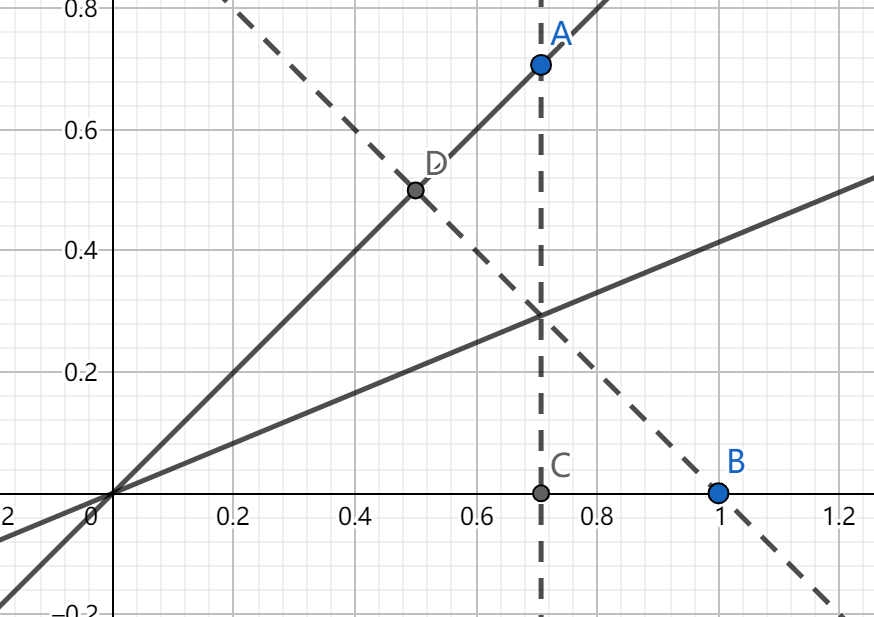
可以发现，经过对称，$x$轴在$\vec e$上的投影长度恰好等于$\vec e$在$x$上的投影。所以，新空间的基可以解释为原空间基在$\vec e$上的投影长度。因此新空间所有点在原空间内均对应着在$\vec e$所确定的直线上的投影。再回来看公式的另一个变形

$$\vec u \cdot \vec v = k\vec e^T \vec v$$

即将新空间内的坐标$\vec v$变换回原空间，即在$\vec e$上的投影长度，再乘以$\vec u$本身的长度$k$。这与点积的计算方式一致。

通过类似的方法也能建立起叉积和线性变换的关系，不过我还没弄明白。

特征向量

另一种看到线性变换的角度就是特征向量。通过特征向量也可以表示一个线性变换。

特征向量是在一次变换内方向不发生改变的数个向量，特征值则表示了在该方向上空间被缩放的比例。再以这种思路去看计算公式

$$ A\vec v = \lambda \vec v \implies (A-\lambda I)\vec v =\vec 0 $$

意义不言而喻。而只有当变换使得空间发生降维的时候，我们才有可能让一个非$\vec 0$向量$\vec v$成为$\vec 0$。所以也就是计算$|A-\lambda I|=0$。

不过有时候求不出特征向量，那就意味着这个变换让所有的向量方向改变。

而特征向量的意义则要根据不同的应用来看。例如上文中以某个轴旋转空间，实际上这个轴就是整个旋转的特征向量所在直线。

引入特征向量后，我们能够玩的特技就又多了点。假设对于一个线性变换M我们得到的特征向量足够张成同维度空间，那么特技是把特征向量当作基，设这个基为$B$，创建一个船新的空间。

那么，如果我们把$\Omega_1$下的向量拿过来在$\Omega$下做$\Omega$下的变换$M$，当把这个变换后的数再次转回$\Omega$下，那么该向量只会在基上发生简单的长度变化。原因在于，新空间的基在$\Omega$下使用$M$变换只会发生放缩而不会改变方向。如果描述为公式的话即下式。

$$ B^{-1}MB=\begin{bmatrix} a & 0 \cr 0 & b \end{bmatrix}=M' $$

这个公式是不是样子非常的眼熟，就是所谓的对角化。我们对$\Omega$下的某个向量$P$做变换，就相当于在$\Omega_1$下对其做$M'$（只有缩放）。

当然，更多的时候就只是仅仅去算某个矩阵的幂$A^n$，那就是将矩阵看作对空间的变换。

$$ D=B^{-1}AB \implies D^n=B^{-1}A^nB \implies A^n=BD^nB^{-1} $$

这显然容易解释通。我们对$\Omega$的变换$A$就相当于在$\Omega1$下进行等价的缩放$D$然后再转回原空间。然而$D^n$由于只有缩放所以对人来讲只要计算对角线上每个数的幂就可以。这也可以用来降低矩阵快速幂的复杂度。